LTspice vs PLECS model of the CAB6R0A23GM4T
Hello,
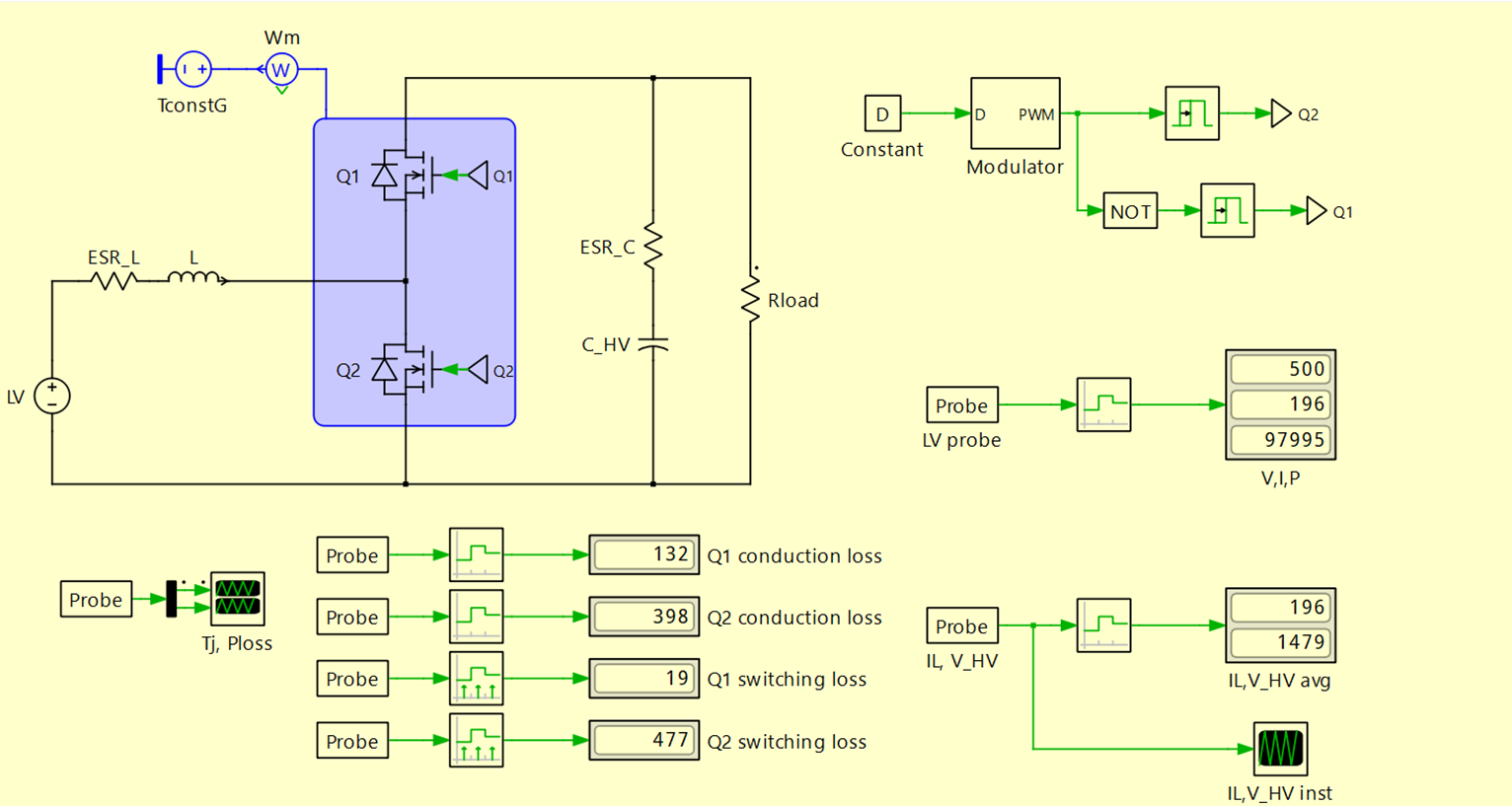
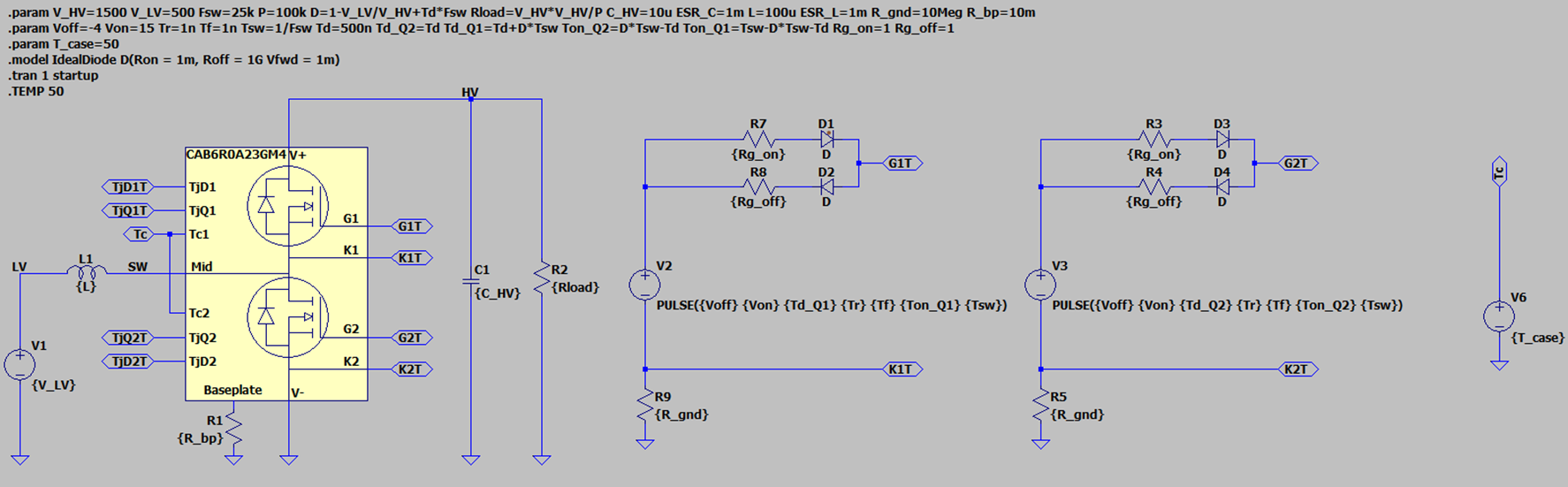
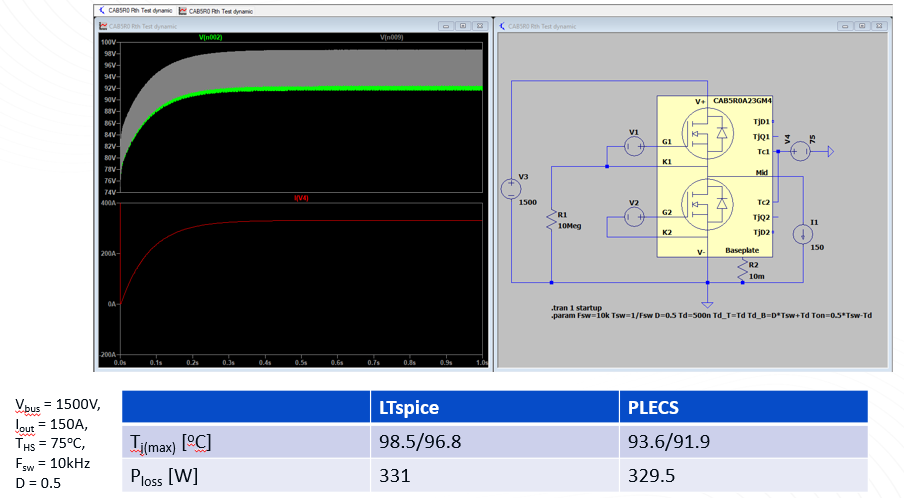
I have been and testing the LTspice and the beta PLECS models of the CAB6R0A23GM4T for the past couple of days and have observed that the losses and junction temperature are pretty different in the two models. With the help of a boost converter test circuit, I have shown in the screenshots below the differences in the simulation outputs from the two platforms. The following simulation conditions have been used:
Input voltage = 500V
Output voltage = 1500V
Power = 100kW
Switching frequency = 25kHz
Rg(ext) = 1 ohm
Case temperature = 50C
I have attached the models in the post for you to take a look at and compare on your end.
PLECS
LTspice
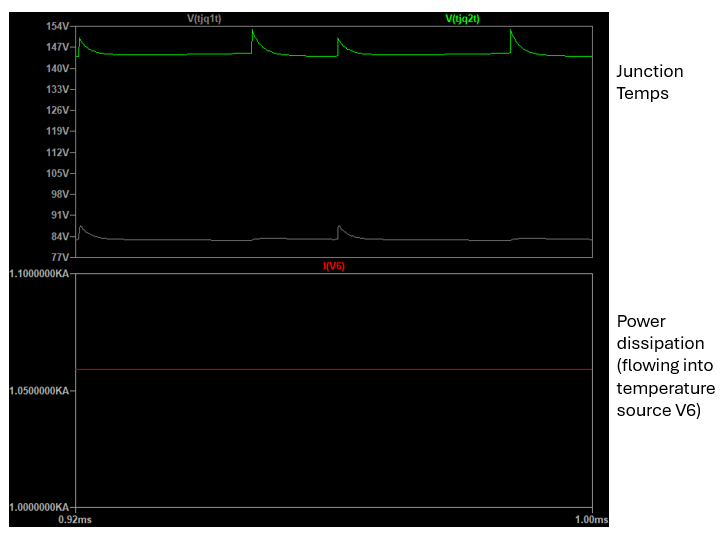
The following table shows the comparison between the recorded junction temperatures and losses. As you can see, there is a significant difference of around 20C in the junction temperature of Q1 and 3-4C in the junction temperature of Q2. There is also a mismatch of losses.
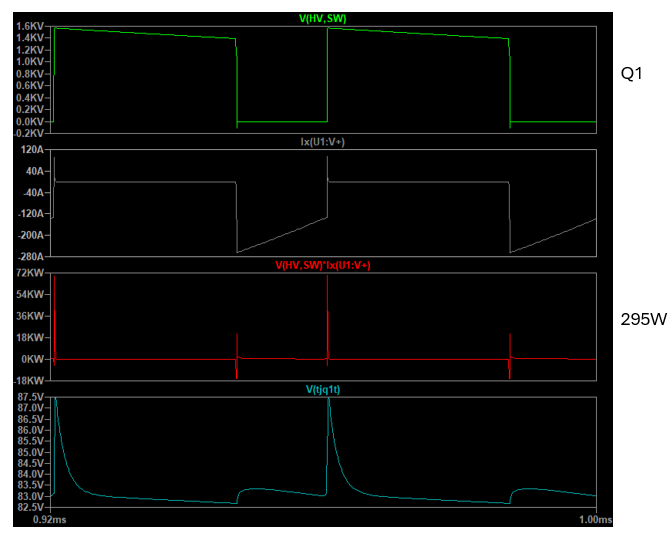
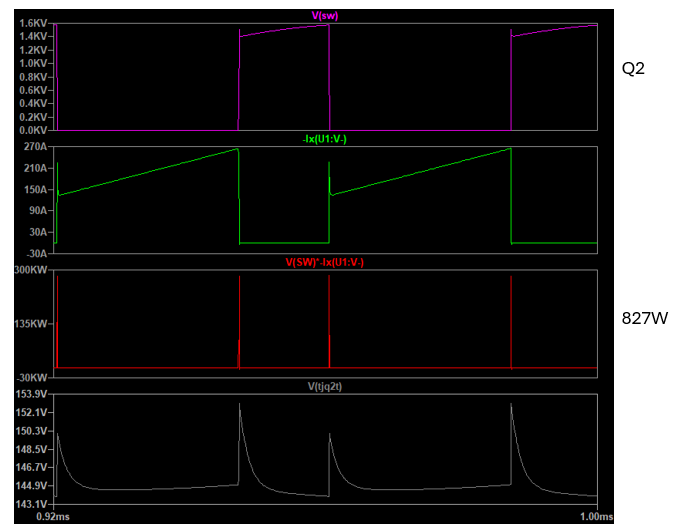
The individual switch losses in LTspice has been computed by plotting the product of the drain-source voltage and the drain current, and then averaging it over two switching cycles, as shown below:
Please not that the sum of the individual switch losses do not add up to the power flowing out of the case port in the LTspice model, which can be seen from the data in the previous table (295+827=1122W, but the power flowing out of the case thermal port is 1058W).
I want to know which model, LTspice or PLECS, is more accurate? Why is there a mismatch between the two simulation results (please take a look at the attached models)? Which simulation result should I trust?
I heavily depend on the temperature calculations for my work, because I am trying to maximize the power output of my converter and am determining the max power output by looking at the maximum junction temperature. I need to know that at least one of the two models is accurate and reliable.
Please let me know what you think.
Regards,
Prathik
Comments
-
Thank you for your post, it has been approved and we will respond as soon as possible.
0 -
Hi Prathik,
I'll need my colleague, Brian, to take a deeper look at the SPICE model to answer your question on the internal loss consistency, but I can answer your more general questions.
I recommend you trust the PLECS model for most simulations. We collect quite a bit of data on our modules, which is then added to the lookup tables in PLECS:
- Double pulse testing to create dynamic loss tables (tested at each Rg, temperature, and voltage in the model; some current points are interpolated / curve fit)
- Curve tracer data to create conduction loss tables
- Transient thermal impedance data (fit by a cauer network)
The datasheet data is actually a subset of the test data we use to build the PLECS models. Because of the lookup tables match our collected data, they represent our best approximation of converter performance for a typical part. Obviously there is also part to part variance to consider, but we do not make the data on variance publicly available. If you'd like help with that kind of simulation, please reach out to your sales representative and I'd be happy to help through official channels.
The SPICE model, on the other hand, is built from our static dataset. We then run a dynamic fitting algorithm which tries to reduce error in the dynamic parameters (e.g. Eon, Eoff, di/dt, etc). This process is never going to get a perfect match across all input variables, so fitting is focused near the nominal values of the device. We would expect a 10-20% match to our experimental data in the region of focus. The error in the SPICE model outside that (switching losses at 200V, for example) could be much higher.
That said, while the PLECS model is generally the correct choice for predicting losses or junction temperature, the SPICE model is far more detailed in the electrical domain (obviously it wouldn't make sense to try to predict overshoot in PLECS). Another caveat to this rule of thumb is that the PLECS models aren't especially accurate at very short timesteps (less than 10 ms). If you are trying to simulate short circuit, for example, I would recommend looking at the SPICE model for losses and temperature.
I hope that information is helpful! We'll get back to you on your SPICE model question.
Thanks,
Blake0 -
Hi Blake,
Once again, thank you for your very detailed response. So the main takeaway from what you've said is that the PLECS model is to be trusted more than the LTspice model for steady state thermal analysis, while LTspice is the go-to platform for electrical analysis.
I need some clarification on what you said about PLECS not being accurate for timesteps lower than 10ms. I did not clearly understand what you meant by this. 10ms is a pretty large timestep and I don't think high frequency converters converters can be simulated at such a high timestep. If my understanding of this is not really correct, could you please explain what this means, because I run all simulations with a maximum timestep setting of not more than Tsw, the period of one switching cycle, which is usually always a lot lower than 10ms? Or are you talking about the timestep of any dynamic behavior of the converter?
0 -
Apologies, I should have double checked my response before posting! My brain took 10e-4 and converted that to 10ms when what I was thinking was 0.1ms. You are correct, inaccuracy at 10 ms would be a huge issue. Additionally, this has nothing to do with the accuracy of the PLECS electrical simulation, merely the quality of fit of the thermal model.
To clarify, in the process of fitting Zth, the small timestep (below 10e-4) data is deprioritized, since we would need a larger thermal networks. In theory this leads to a more robust simulation and faster simulation speed. Here is an example fit for one of our models:
In practice, these means that the accuracy of the predicted junction temperature is lower for very short simulations, but it will be accurate for line frequency perturbations and steady state. From my testing, even the peak junction temperature is not majorly affected by this inaccuracy in many situations. As we are prioritizing models that can work universally, we accept this tradeoff. But this is why, for short circuit and similar simulations, our SPICE model can be a better option.
If you'd like to play around with it, you can easily import our Zth curves into PLECS and fit a very high order thermal network.
Sorry for the confusion! Please let me know if I can provide any additional clarifications.
Thanks,
Blake0 -
Hi Blake,
I understood what you mean now. So does this mean that the peak junction temperature calculation is slightly inaccurate at switching instants? When I was comparing the LTspice and PLECS models of the 5R0 power module, I noticed that although the losses were equal, the peak junction temperatures were different in the two simulation platforms.
When designing converters, I usually maximize the power output until the peak junction temp hits the maximum temperature specified in the datasheet. Putting part-to-part variations aside, does PLECS calculate a slightly lower peak junction temp during switching events compared to the actual power module? If so, how many degrees of safety margin should I assume? Also, in stead state and at max power, is it more important to check if the peak temperature is below the limit, or the average?
0 -
Certainly, there is a bit of inaccuracy for the near instantaneous power loss of the switching event. Of course, if you are getting to very small time steps (<1e-6), even the confidence in the thermal impedance data drops.
I would argue, however, that the precise temperature for very short durations is mostly irrelevant to system design. In reliability testing, the duration of the pulse plays a large role in the number of cycles survived, with short on-pulses leading to much large cycle counts (the typical pulse timing is 1 second on, 1 second off, I believe). In other words, device degradation is dependent not only on the magnitude of the temperature delta, but also the duration of the cycle.
This means that if you are using the peak junction temperature in PLECS, you are already being conservative, as the average temperature is more relevant to calculating device lifetime (the maximum delta between your case temperature and average junction is used to estimate lifetime). I wouldn't necessarily recommend adding in a fixed margin: semiconductor devices do not die instantaneously when slightly above their max junction temperature, instead, degradation scales with the size of the temperature delta. Reducing your average temperature from 70C above fluid to 60C might double your lifetime, but the small error in peak temperature is usually going to be far less relevant due to its very short duration.
 0
0 -
Hi, I hope that this answered your question. I will close this discussion for now but if you have a follow up question, please "Start a New Discussion" and we would be glad to support you further.
0