Abaout of CCB021M12FM3 Power Dissipation

Omer

Hi there,

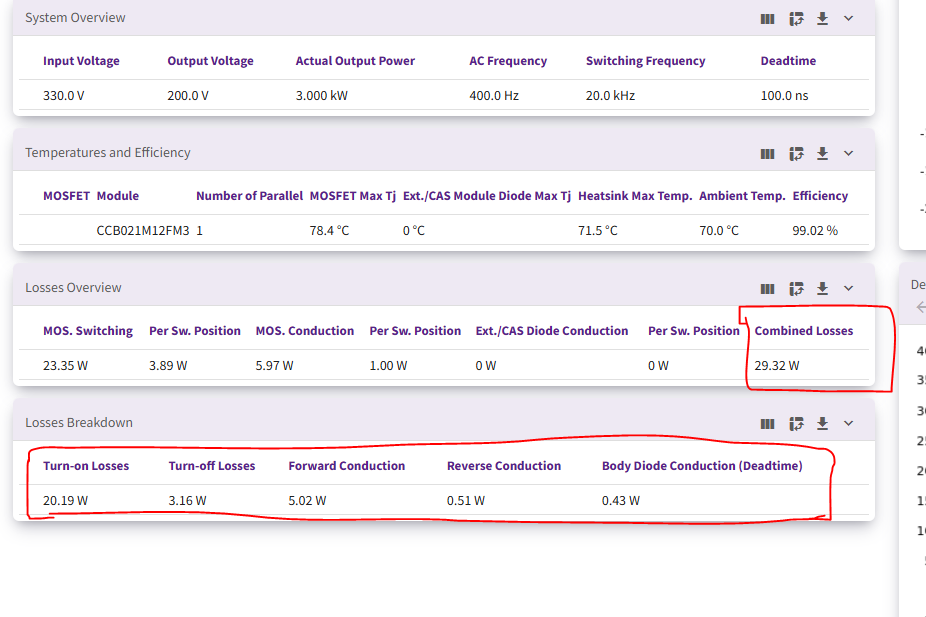
I am calculating and simulating the power dissipation of a three-phase, two-level inverter using the CCB021M12FM3 sixpack MOSFET module. Initially, I used the SpeedFit design simulator, which indicated combined losses of 29.32W.

Does this result represent the losses for a single MOSFET in the sixpack? I also simulated the circuit in LTspice and observed approximately 30W of power loss per MOSFET. By measuring the input and output power difference in LTspice, I calculated the total power dissipation for the entire sixpack to be six times the individual MOSFET loss, amounting to around 180W.

Is this conclusion correct? Please could you quick reply, thank you.

Forum_Moderator

Thank you for your post, it has been approved and we will respond as soon as possible.

BlakeNelson

Hello Omer,

The "Per Sw. Position" losses (for both switching and conduction) are about 1/6 the "MOS. Switching" or "MOS. Conduction" value. And the sum of "MOS. Switching" or "MOS. Conduction" equals the combined value. So its safe to assume the combined losses consider all 6 switch positions.

The small losses makes sense for how lightly loaded the module is (8.7 A, 330V). For a quick validation, we can see from the datasheet voltage drop at 10 amps is less 0.2V, which would indicate that ~1W of conduction losses would make sense. For switching, we see Etot ~= 0.35 mJ at 600V, 10A. At 330V, that should be more like 0.2 mJ, so 0.2 mJ*20 kHz = 4 W. These estimates line up reasonably well with your results from SpeedFit (especially since I just eyeballed the datasheet).

So my best guess would be that there is some difference between the simulations leading to this large delta. If you would like to share your SPICE model, perhaps we could help you troubleshoot it?

Hopefully that is helpful!
Blake

Omer

Hello Nelson,

I agree with your assessment; however, the assumed external gate resistor (R_Gate (ext)) is 0 Ω. If we do not use an external gate resistor, the EMI noise will increase. Could you assist me in calculating the power consumption of the six-pack module based on the parameters provided below?

VDS: 330V

Rgate(ext) = 14R (both are same turn of and turn on)

Fsw=20kHz

Vout_Line_Line=200VAC or (Phase to neutral voltage is 115VAC)

Pout=3000W

Inductance= 300uH

Grid_Frequency=400Hz

T_ambiant = 100°C (The ambient temperature is 70°C, but we assume it to be 100°C due to heat generated by other components in the equipment.)

I am trying to calculate the power loss in a sixpack module, but I couldn't find results similar to your simulation. Could you let me know if my calculations are correct? If not, could you share your sixpack power loss calculation with me?

Eon= 0,5mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Eon= 0,5mj x (1,05) = 0,525mj @100°C
Eon= 0,5mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Eon= 0,5mj x (8,7A/30A)=0,316mj @8,7A
Eon= 0,5mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Eon= 0,5mj x (2,12) = 1,06mj @ Rg=15 Ohm
Eon= 0,5mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Eon= 0,5mj x (330/600) = 0,275mj @ 330V
So that; Eon= 0,5mj x (1,05) x (8,7/30) x (2,12) x (330/600) ~= 0,18mj

Eoff= 0,02mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Eoff= 0,02mj x (1,75) = 0,035mj @100°C
Eoff= 0,02mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Eoff= 0,02mj x (0,85)=0,017mj @8,7A
Eoff= 0,02mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Eoff= 0,02mj x (12) = 0,24mj @ Rg=15 Ohm
Eoff= 0,02mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Eoff= 0,02mj x (330/600) = 0,275mj @ 330V
So that; Eoff= (0,02) x (1,75) x 0,85 x 12 x (330/600) ~= 0,20mJ

Err= 0,14mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Err= 0,14mj x (1,107) = 0,155mj @100°C
Err= 0,14mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Err= 0,14mj x (0,286)=0,04mj @8,7A
Err= 0,14mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Err= 0,14mj x (0,071) = 0,01mj @ Rg=15 Ohm
Err= 0,14mj (@25°C, @30A, 600V and @Rg= 0 Ohm) ==> Err= 0,14mj x (330/600) = 0,275mj @ 330V
So that; Err= 0,14 x (1,107) x (0,286) x (0,071) x (330/600) ~=0mJ

Switching losses per MOSFET= (Eon + Eoff + Err)* Fsw = ( 0,18mj + 0,20mJ + 0mj ) x 20Khz = 7,6W (per MOSFET)

Conduction Losses:

RdsOn = 34,875 mOhm (@100°C)

P_cond_loss = Irms * Irms * RdsOn / 1000 = 8,7 x 8,7 x 34,375 /1000 ~= 2,64W (per MOSFET)

P_sixpack_total_loss= (7,6W + 2,64)*6 ~= 61,44 W

BlakeNelson

Hey Omer,

I think your analysis approach makes sense, though the stacking of all the scaling factors is likely going to lead to some inaccuracy (for example, scaling with current is not perfectly linear). As we are pretty far from the nominal datasheet conditions, I would expect relatively high error on this estimation (SpeedFit will also have relatively high inaccuracy at these conditions). Similarly, 34.9 mΩ is likely a bit high for typical resistance at 100°C, <10 A. Based on figure 2 of the datasheet, I think 21*1.2 = 25.2 mΩ would make sense for typical (maybe you were thinking max? but typical would match SpeedFit, if that is the concern), though that would predict 1.9 W per MOSFET which still isn't a perfect match with SpeedFit.

The test conditions you are interested in are well below the ratings of the modules, and the models we provide aren't optimized for accuracy in this region. From a capability perspective, 10W per switch position is well within the thermal limit of the module, so even if the losses are not quite right, we can be confident the module is capable handling of your conditions.

If you need an accurate loss estimate for efficiency purposes, I would recommend proceeding with the analytical approach you have shown. It may be helpful to have our switching test results for the 15 Ω testing as this is not included in our datasheet:

Switching Energy (mJ)

VDS = 600V
TJ = 025C	
RG = 15 Ω

ID	EOFF	EON	ED-RR

5	0.03	0.38	0.00

10	0.07	0.50	0.00

15	0.10	0.62	0.00

20	0.14	0.75	0.01

25	0.18	0.89	0.01

30	0.23	1.03	0.01

35	0.27	1.18	0.01

40	0.32	1.33	0.01

45	0.36	1.48	0.01

50	0.41	1.64	0.01

55	0.46	1.80	0.01

60	0.51	1.97	0.01

65	0.57	2.15	0.01

70	0.62	2.32	0.01

75	0.68	2.51	0.01

80	0.74	2.70	0.01

85	0.80	2.89	0.01

90	0.86	3.09	0.01

95	0.92	3.29	0.01

100	0.99	3.50	0.01

You'll still need to scale for voltage and temperature, as we do not test below 600V and only tested at 25 °C for high gate resistance. Switching losses below 0.1 mJ are near the limit of our test resolution, so even this approach will have some error, but it should be more accurate than SpeedFit for your conditions.

Let me know if I can provide any other information.

Thanks,

Blake